Structural Finite Element Analysis (SFEA) is a method by which the structural response of a component is simulated. FEA CAN:
Provide validation of the structural performance of a component. Allow several iterations of design to be ‘tested’ in advance of tooling Help to optimize a part by minimizing material usage.
In the case of metal to plastic translations, the SFEA is of critical importance.
|
The process itself starts with a predefined geometry. The part is then “meshed,” or broken into a series of smaller pieces, which represent the geometry. After loads and constraints are applied and material properties defined, the problem is solved
|


 Creating and running the model is only the beginning. The most important aspect of a structural FEA is the interpretation of results and using this information to develop improved designs. As a customer, you get maximum value out of an analysis when questions other than “Will it fail?” are answered.
Creating and running the model is only the beginning. The most important aspect of a structural FEA is the interpretation of results and using this information to develop improved designs. As a customer, you get maximum value out of an analysis when questions other than “Will it fail?” are answered.

You Should expect these questions to be answered as well:
|
If the part fails, what is the best way to reinforce it?
|
|
Is there an opportunity to “cost reduce” this part by removing material?
|
|
Based on the results, is there a more “material efficient” design that will achieve the same performance?
|

Depending on the type of results required, there are several different types of analysis runs:
Linear Static Analysis :
This is the fastest and most common analysis run. It simulates the structural response of the component under prescribed loading at equilibrium. Linear analysis is accurate within its realm; large deflections and nonlinear materials cannot be modeled accurately.
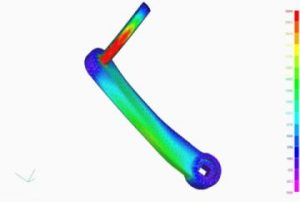
Non-linear static analysis simulates the structural performance of a static load case involving either or both of the following:
|
1. Large part deflections
|
|
2.Materials which do not have a constant stiffness with increasing strain
|
|
3. Contact Analysis
|
|
These analyses are more time-intensive, both in terms of creating the model and solving time. Using a planar element rather than a solid will save solving time, but will likely require additional time in creating the model. It is generally wise to start with a linear analysis to verify the need for a non-linear analysis.
|
|
|
This analysis predicts the natural frequencies of the part and the mode shapes associated with each frequency. These results are very important in the automotive industry, where the elimination of noise/vibration/harmonics leads to a quieter ride. In other industries, it is used to identify the frequency at which a component will vibrate excessively, often with catastrophic results.
|

